Fast Forward Modeling

One of the most important areas of the CEMI research is fast and accurate forward electromagnetic modeling. There are several techniques available for electromagnetic forward modeling. They are based on numerical implementation of the differential equation (DE) approach (finite difference, FD, or finite element, FE, methods) or the integral equation (IE) approach. In the CEMI research we develop multi-dimensional (2-D, 2.5-D, 3-D) forward modeling methods and computer codes based on different mathematical methods.

The integral equation (IE) method has been proven to be an efficient tool to model three-dimensional electromagnetic problems. Due to the full linear system of equations to be solved, the method was considered in the past to be effective only in the case of models consisting of a limited number of cells. As a result, the integral equation method was used mostly in the model study with the conductivity anomalies restricted to a few numbers of rectangular blocks. However, recent advances in matrix storage and multiplication issues facilitate the modeling of large structures, using iterative methods for matrix inversion. We also introduce a new Contraction Integral Equation method, which improves the convergence rate of the iterative solvers dramatically (Hursan and Zhdanov, 2002). The new integral equation based computer code INTEM3D can be used for accurate modeling 3-D EM fields in complex structures with large-scale conductivity variations. It posses flexibility in forward simulations compatible with the flexibility of FD modeling, but preserves the high level of accuracy typical for IE techniques. Due to the advanced storage reduction and FFT-based matrix multiplications, incorporated in this program, it is possible to obtain full IE solutions for large models containing several thousand cells.

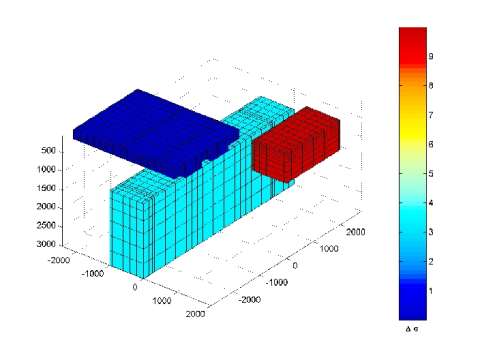
We will present below, as an illustration, a forward modeling result based on INTEM3D software package. The model is one of the new generations of 3-D models of the COMMEMI project (Varentsov et al., 2000). It consists of seven conductive blocks (Figure 1). Five of them are adjacent in the y-direction and are elongated in the x-direction, forming a subsurface syncline-like structure. These blocks have the same size of 3 km in the x-direction, while their sizes in the y- and z-directions (from body 1 to body 5) are different and equal to 0.4, 0.6, 0.4, 0.6 and 0.4 km, and 0.4, 0.6, 0.4, 0.6 and 0.4 km respectively. The resistivities of these blocks (from 1 to 5) are 300, 30, 100, 30 and 300 Ohm-m. The background vertical section of the model consists of three layers with resistivities of 1000, 10000 and 10 Ohm-m, and with thickness of the first and the second layers of 1 and 6.5 km respectively. The observation region and periods selected for the comparison, are [-40,40]X [-40,40] km{2} and 0.1, 1, 10 and 100 s. This model combines a high conductivity contrast up to 30,000 with the anomalous structure almost outcropping at the ground surface. This model is quite typical both for mining EM applications and for regional MT studies. It requires a large grid to approximate all the structures with the proper resolution.

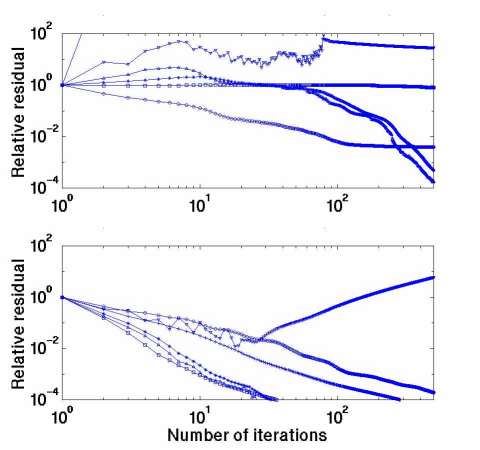
Figure 1. A sketch of 3-D geoelectrical model consisting of several conductive blocks within a layered medium excited by a plane-wave source (after Varentsov et al., 2000).

We have performed a comparative study of the convergence of different iterative solvers applied to the original and contraction integral equations. The solvers we used for the conventional IE and CIE methods include 1) the Successive Iteration (SI) method, 2) the Conjugate Gradient Normal Equation Residual (CGNR) method, 3) the Biconjugate Gradient (BICG) method, 4) the Biconjugate Gradient Stabilized (BICGSTAB) method, 5) a quasi-minimal residual variant of the BiCGSTAB (QMRCGSTAB), and 6) the Complex Generalized Minimum Residual (CGMRES) algorithms.

The history of the relative residuals during the iterations is plotted in Figure 2. The upper panel shows the behavior of the relative residual errors of the different iterative solvers applied to the conventional integral equation. The bottom panel presents the same plots obtained for the contraction integral equation (CIE). The convergence rate in the last case is significantly higher than in the case of the conventional integral equation method.

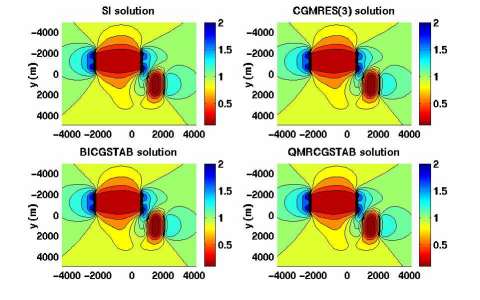
Figure 3 presents the comparison of the x-component of the electric field for a period of 1 s obtained with the different solvers based on the CIE method.

Figure 2. Behavior of the relative residual errors during the iterations for the conventional IE method (top panel) and for the contraction IE method (bottom panel) for the 3-D modeling experiment (after Hursan and Zhdanov, 2002)

Figure 3. Amplitude of the x-component of the electric field at the surface obtained for a period of 1 s obtained by solving CIE by four different solvers. The results have been normalized to the background electric field (after Hursan and Zhdanov, 2002).

Over the last several years CEMI developed a family of linear and nonlinear approximations for electromagnetic modeling in conductive inhomogeneous media. (Zhdanov and Fang, 1996, 1997, 1999; Zhdanov et. al., 2000). These approximations form the basis for high-performance forward modeling and inversion methods. The new computer code INTEM3D includes forward modeling routines based on the Born approximation, quasi-analytical approximation and series, full integral equation and contraction integral equation methods. The INTEM3D software package makes it possible to generate electromagnetic field for the following set of the different sources:

- plane wave propagating vertically toward the earth (magnetotelluric);
- current bipoles along the x, y and z directions;
- horizontal rectangular loop;
- horizontal circular loop;
- moving horizontal loops;
- magnetic dipoles oriented in the x, y and z directions.

The options for calculating the Born and QA approximations and series are designed for quick modeling of excessively large structures.

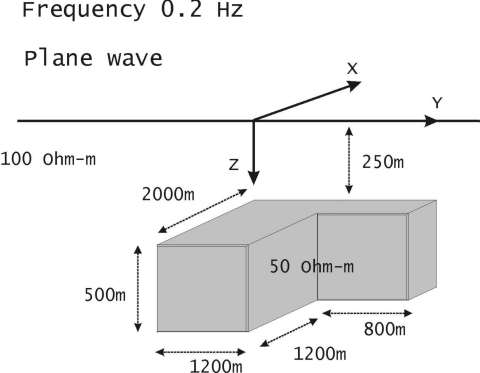
Figure 4. A model study of the QA approximation (after Tolstaya et al., 2002).

As an illustration of the accuracy of the QA approximation, we consider a geoelectrical model shown in Figure 4. The model is excited by the plane wave. We computed the magnetotelluric impedances for this model using rigorous solution based on the CIE method and QA approximation.

Figure 5 shows the maps of the nominal TE mode component of the impedance tensor. The top panel presents the full integral equation (rigorous) solution, while the bottom panel presents the same result obtained by the QA approximation. The calculations were performed by the INTEM3D code.

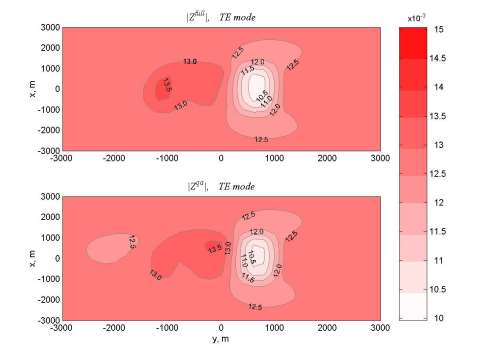
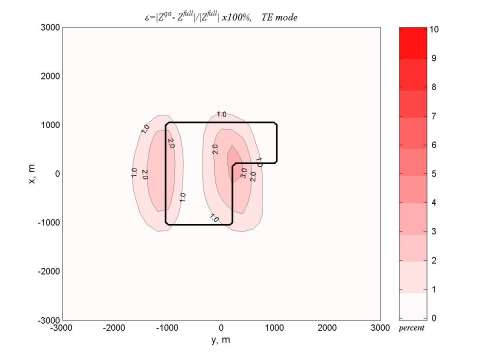
Figure 5. The maps of the nominal TE mode component of the impedance tensor computed using the full integral equation method (top panel) and the QA approximation (bottom panel) (after Tolstaya et al., 2002).

Figure 6 shows the relative errors of the approximate solution. One can see that for this model the errors do not exceed 3%. Note that for the more complicated geoelectrical model with the high conductivity contrast these errors may increase up to 8-10%, however, application of the QA approximations of the higher order (which is another option of the INTEM3D code) helps to reduce these errors to the required level of accuracy.

Figure 6. The maps of the relative errors of the QA approximation. (after Tolstaya et al., 2002).

Recently, CEMI has developed a new approach for multi-source three-dimensional (3-D) finite difference (FD) electromagnetic (EM) modeling in the frequency domain. This approach is based on the balance method, solves for the anomalous electric field, and automatically takes into account the conservation law of Maxwell's equations. We also use a new boundary condition based on the quasi-analytical (QA) approximation/series in order to truncate the 3-D FD modeling grid in both air and earth (Mehanee and Zhdanov, 2002, 2003). The QA-based Dirichlet boundary condition resulted in good computational accuracy. This approach helps reduce the size of the modeling grid significantly without loosing any accuracy of calculation. As a result, the larger number of the grid cells can be used to describe the anomalous conductivity distribution within the modeling domain.

The new CEMI finite-difference forward modeling software package FDEM3D may be used for simulating the electromagnetic field generated by the same set of the different sources as in the INTEM3D package. The developed finite difference code is designed for different geophysical applications, including magnetotelluric (MT), controlled source magnetotelluric (CSMT), airborne, and borehole EM methods in the frequency domain.

Hursan, G. and M. S. Zhdanov, 2002, Contraction integral equation method in 3-D electromagnetic modeling: Radio Science, 37, No. 6, 1089.

Mehanee, S. and M. S. Zhdanov, 2003, Quasi-analytical boundary conditions in 3-D electromagnetic modeling: Journal of Computational Physics: Proceedings of 2002 CEMI Annual Meeting, 15-42.

Mehanee, S. and M. S. Zhdanov, 2003, 3-D finite difference electromagnetic modeling based on the balance method and quasi-analytical boundary conditions: Journal of Computational Physics, submitted.

Tolstaya, E., Yoshioka, K., and M. S. Zhdanov, 2002, Accuracy study of quasi-analytical and quasi-linear approximations for 3-D electromagnetic field: Proceedings of 2002 CEMI Annual Meeting, 43-86.

Varentsov, I. M., Fomenko, I. Y., Golubev, N. G., Mehanee, S., Hursan, G., and M. S. Zhdanov, 2000, Comparative Study of 3-D Finite Difference and Integral Equation Methods: Proceedings of 2000 CEMI Annual Meeting, 35-74.

Zhdanov, M. S. and Sh. Fang, 1996, Quasi-linear approximation in 3D electromagnetic modeling: Geophysics, 61, No 3.

Zhdanov, M. S. and Sh. Fang, 1997, Quasi-linear series in 3-D electromagnetic modeling: Radio Science, 32, No. 6, 2167-2188.

Zhdanov, M. S. and Sh. Fang, 1999, 3D quasi-linear electromagnetic modeling and inversion: Three-dimensional Electromagnetics, ed. By M. Oristaglio and B. Spies, 1999, Geophys. Devel. Ser., No. 7, Soc. Explor. Geophys., Tulsa, 724 pp.

Zhdanov, M. S., Dmitriev, V,I,. Fang, Sh., and G. Hursan, 2000, Quasi-analytical approximation and series in 3D electromagnetic modeling: Geophysics, 65, 1746-1757.

Zhdanov, M.S. 2002, Geophysical inverse theory and regularization problems: Elsevier, Amsterdam - New York - Tokyo, 628 pp.