

 |
 |
Rapid 3-D interpretation of magnetotelluric data
By Michael S. Zhdanov, Ekaterina Tolstaya and Nikolay Golubev
Interpretation of magnetotelluric data over inhomogeneous geological structures is still a challenging problem in geophysical exploration. CEMI has developed a rapid 3-D MT inversion method and a computer code based on full nonlinear conjugate gradient inversion and quasi-analytical (QA) approximation for forward modeling solution (Rapid 3-D magnetotelluric inversion). Application of the QA approximation to forward modeling and Frechet derivative computations speeds up the calculation dramatically. However, in order to control the accuracy of the inversion, our method allows application of rigorous forward modeling in the final steps of the inversion procedure. The main distinguishing feature of this algorithm is application of the smooth or focusing stabilizing functionals that allow construction of both smooth images of underground geoelectrical structures and models with sharp geoelectrical boundaries. The 3-D magnetotelluric inversion code has been carefully tested on synthetic models and applied to the practical MT data collected in an area with complex geology. The rapid inversion of the array magnetotelluric data (observed with hundreds of multi-frequency observation stations) can be done within a few minutes on a PC to generate the full 3-D image of subsurface formations on a large grid with tens of thousands of cells.
The original QAINV3Dcode has been modified recently by implementing a specially designed nonlinear parameterization of the model parameters, which improves the convergence rate of the algorithm (Zhdanov and Tolstaya, 2003). A new version of the code uses the quasi-analytical approximation as a forward operator (Zhdanov et al., 2000) in the initial stage of inversion and the rigorous contraction integral equation based forward modeling at the final stage of inversion (Hursan and Zhdanov, 2002).
We present below some numerical examples of the MT data inversion with this new code.
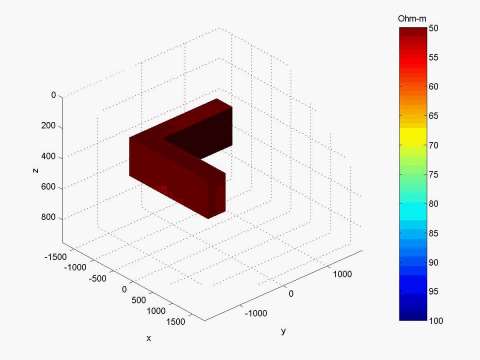
Model 1: L-shape conductive structure
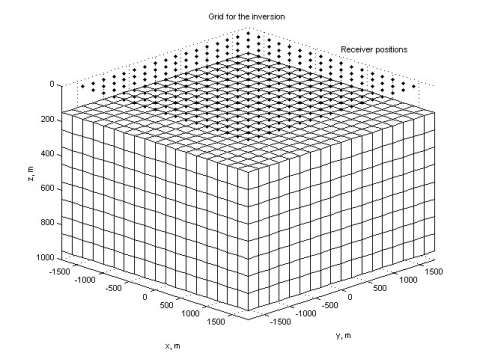
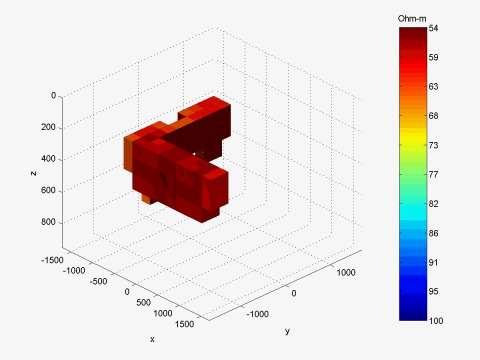
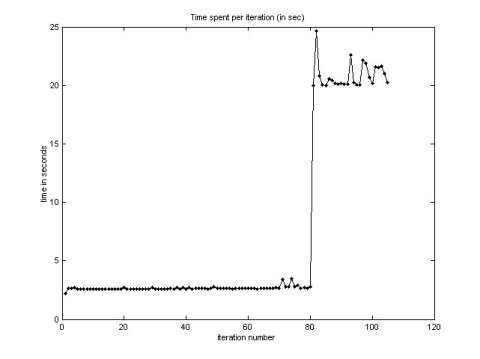
Figure 1 presents am L-shape conductive structure. The discretization grid and MT station positions for this model are shown in Figure 2. A 3-D image of the inversion result is shown in Figure 3. The computational time for every iteration is presented in Figure 4. One can see that one QA iteration requires just a few seconds of computation; while one rigorous iteration based on the Contraction Integral Equation forward modeling requires about 20 seconds per iteration. The recovered image reconstructs well the original model.
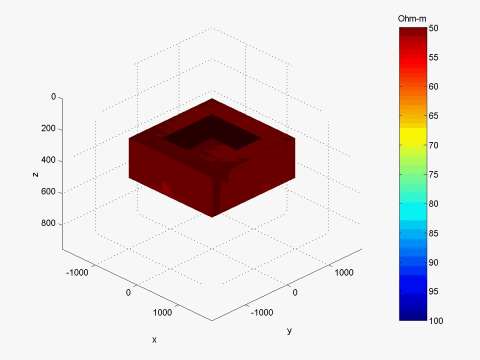
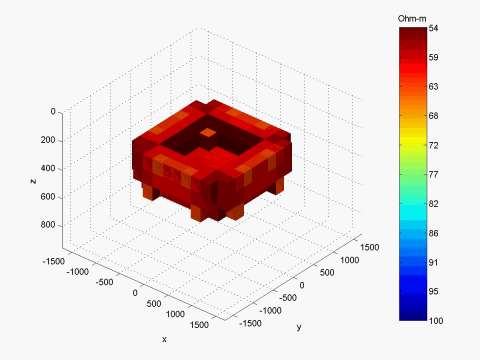
Model 2: "Open box" conductive structure
We present a similar result for the "open box" model shown in Figure 5, simulating a conductive syncline structure. The inversion of the MT data simulated over this model is presented in Figure 6.
Inversion of the Voisey’s Bay data
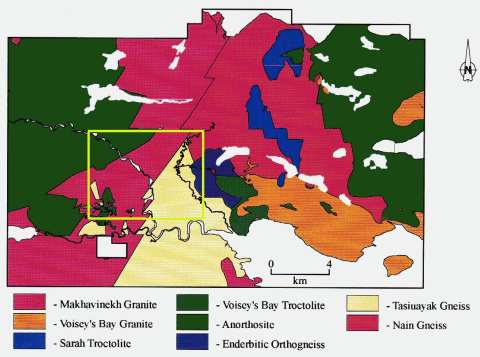
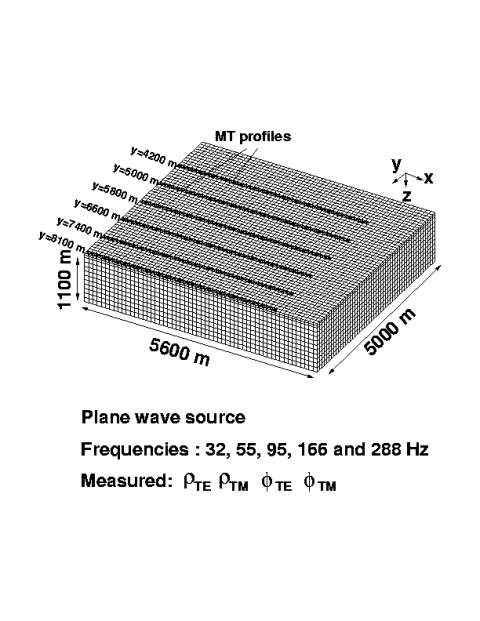
The case study presented here involves interpretation of the results of an array magnetotelluric survey consisting of eleven profiles covering an area of about 28 km^2, collected by INCO Exploration at the Voisey's Bay area, where massive sulfide deposits were discovered (Naldrett et al., 1996; Balch, 2000). The deposits are hosted by troctolite dikes that are thought to be feeder conduits for the Voisey's Bay intrusion of the Nain Plutonic Suite (Naldrett et al., 1996).
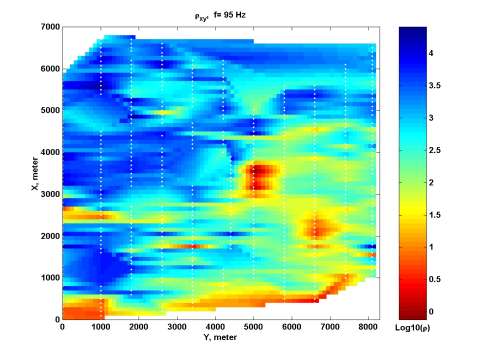
The boundaries of the magnetotelluric survey are shown in Figure 7 by a bold yellow line. The 3-D MT survey consists of eleven lines passing from the South to the North. The frequency range of MT data is from 10 Hz to 350 Hz. We use for inversion two off-diagonal elements of the impedance tensor, Zxy and Zyz at five different frequencies between 32 Hz and 288 Hz (288 Hz, 166 Hz, 95 Hz, 55 Hz, and 32 Hz). For example, Figure 8 presents a map of Zyz apparent resistivity for a frequency of 96 Hz. We can see clearly the location of the anomalous zone in this map.
The area of inversion consists of 56 X 50 X 12 = 33600 cells. Figure 9 presents the 3-D view of the area of inversion and its discretization.
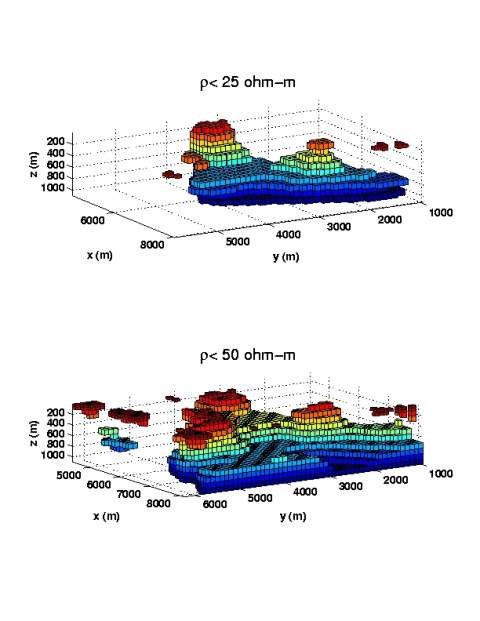
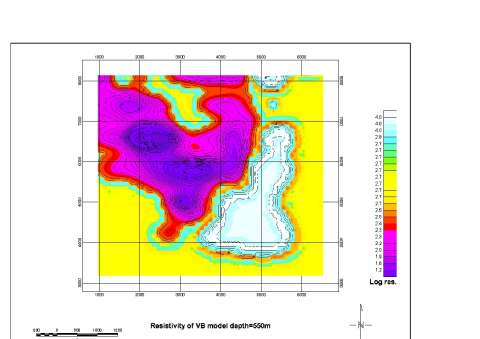
As a result of the inversion, we obtained a volume distribution of electrical resistivity under the area of about 28 km^2 to a depth of 1 km. Figure10, top panel, shows 3-D conductive bodies with resistivity below 25 ohm-m, while Figure 10, bottom panel, presents the domains with resistivity below 50 ohm-m. One can see a conductive anomaly with a complex shape in Figure 10 reaching a depth of several hundred meters. We have plotted also the horizontal map at the different depths of the resistivity obtained as the result of the inversion. These maps are generated using the Geosoft package. An example of this map at a depth of 550 m is shown in Figure 11.
REFERENCES
Golubev, N. G., and M. S. Zhdanov, 2003, Three-dimensional MT inversion over complex geological structures: Proceedings of 2003 CEMI Annual Meeting, 347-382
Hursan, G. and M. S. Zhdanov, 2002, Contraction integral equation method in 3-D electromagnetic modeling: Radio Science, 37, No. 6, 1089.
Balch, S. J., 2000, Geophysics in mineral exploration: fundamentals and case histories. Ni-Cu sulphide deposits with examples from Voisey's Bay: in Practical Geophysics III, Northwest Mining Association.
Naldrett, A. J., Keats, H., Sparkes, K., and S. Moore, 1996, Geology of the Voisey's Bay Ni-Cu-Co Deposit, Labrador, Canada: Explor. Mining Geol., 5, 169-179.
Zhdanov, M. S., and E. Tolstaya, 2003, Three-dimensional inversion of array MT data with minimum support nonlinear parameterization: Proceedings of 2003 CEMI Annual Meeting, 329-346.
Zhdanov, M. S., Dmitriev, V,I,. Fang, Sh., and G. Hursan, 2000, Quasi-analytical approximation and series in 3D electromagnetic modeling: Geophysics, 65, 1746-1757.